МИНИСТЕРНСТВО ОБРАЗОВАНИЯ РОСИЙСКОЙ ФЕДЕРАЦИИ

ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра “Автоматизация производственных процессов”

Методические указания к лабораторной работе №1

“Исследование распространения сигналов в длинных линиях”

по курсу

“Передача данных в информационно-управляющих системах”

для студентов специальности 2101

Ростов-на-Дону

2001 г.

Составители: к.т.н. Кочетов А.Н., к.т.н. Назаренко Д.В.

Методические указания к лабораторной работе №1 “Исследование распространения сигналов в длинных линиях” по курсу “Передача данных в информационно-управляющих системах”/ДГТУ. Ростов-на-Дону, 2001 г.

Печатается по решению методической комиссии факультета “Автоматизация и информатика”

Рецензент: к.т.н. Семко И. А.

Издательский центр ДГТУ, 2001

Исследование распространение сигналов в длинных линиях

Цель работы: ознакомится с основными положениями теории длинных линий и её важнейшими следствиями, а также исследовать и описать процессы распространения сигналов в таких линиях.

Краткая теория:

1. Линии передачи. Параметры линий передачи. Эквивалентные схемы.

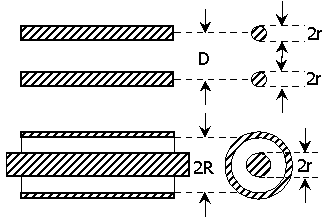
Линии, предназначенные для передачи энергии электрических колебаний от источника (генератора) к потребителю (нагрузке), принято называть линиями передачи или передающими линиями. Конструктивно передающие линии могут быть выполнены множеством различных способов, однако на практике в качестве таких линий чаще всего используются так называемые двухпроводные и коаксиальные линии (рис. 1).

Рис. 1. Продольный и поперечный разрезы двухпроводной
и коаксиальной линий.

Если размеры и форма поперечного сечения линии, диэлектрическая среда, в которую она помещена, и материал проводников в любом сечении линии остаются одними и теми же, то линия называется однородной или регулярной. Как и любая другая система металлических проводников, передающая линия обладает некоторыми значениями индуктивности L, активного сопротивления R, ёмкости С и активной проводимости G, обусловленной несовершенством окружающего линию диэлектрика. Однако эти параметры не сосредоточены на каком-то определённом участке линии, а распределены по всей её длине. Поэтому в отличие от цепей с сосредоточенными параметрами, у которых величины L, R, C и G всегда локализованы в соответствующих пространственно разделённых элементах, передающие линии являются цепями с распределёнными параметрами.

В регулярных линиях передачи величины L, R, C и G распределены вдоль линии равномерно. Учитывая это, можно ввести линейные плотности указанных параметров (так называемые “погонные параметры”), определив их отношениями

где l – геометрическая длина линии. Тогда для любого бесконечно малого участка линии Dх соответствующие ему величины DL, DR, DC и DG могут быть выражены через “погонные параметры” соотношениями.

При этом эквивалентную схему бесконечно малого участка линии Dх можно представить в виде цепи, содержащей сосредоточенные элементы DL, DR, DC и DG (рис. 2), а эквивалентную схему всей линии – в силу того, что любой участок регулярной линии полностью идентичен любому другому её участку – в виде достаточно большого числа таких звеньев, включённых каскадно. Примечательно, что если такую схему собрать из сосредоточенных элементов, численные значения которых равны соответственно DL, DR, DC и DG, то в области низких частот она будет обладать всеми свойствами реальной передающей линии. Такого рода схемы получили название искусственных линий и находят применение в современной радиоэлектронике.

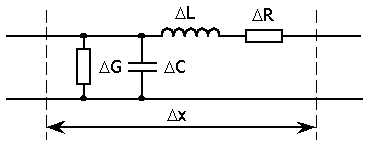
Рис. 2. Эквивалентная схема бесконечно малого участка линии DX.

2. Длинные линии передач. Дифференциальные уравнения длинных линий.

Линия передачи считается длинной, если её электрическая длина

(e и m - соответственно диэлектрическая и магнитная проницаемости среды, в которую помещена линия) соизмерима и тем более превосходит длину волны l передаваемого по линии электрического сигнала. Важнейшей особенностью длинной линии является то, что в каждый данный момент времени напряжения, и токи в различных её сечениях оказываются различными. Например, у линии с электрической длиной l_эл=l/4, возбуждаемой от генератора синусоидальных колебаний, в те моменты времени, когда на одном её конце напряжение обращается в нуль, на другом оно достигает максимума (рис. 3).

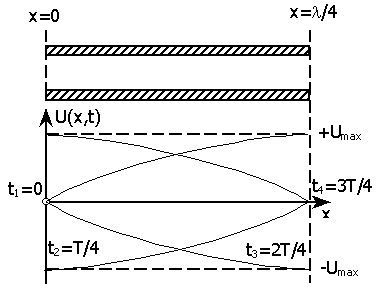
Рис. 3. Диаграмма изменения напряжения в лини l_эл=l/4.

А это означает, что электрические процессы в длинных линиях всегда нестационарны и поэтому для цепей, в которые эти линии входят в качестве составных элементов, уравнения Кирхгофа неприменимы. Вместе с тем, для бесконечно малых участков длинных линий, размеры которых Dх удовлетворяют условию

(напомним, что это условие называется условием квазистационарности) указанные уравнения сохраняют силу, и это позволяет сравнительно простыми средствами, не прибегая к решению дифференциальных уравнений Максвелла, выяснить характер распространения электрических колебаний в длинных линиях.

В самом деле, свяжем начало координат с плоскостью включения нагрузочного сопротивления линии Z_Н , направив ось х влево от этой плоскости (рис. 4).

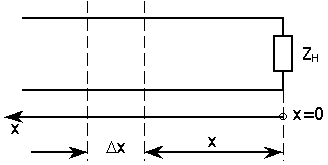
Рис. 4. Схема подключения нагрузочного сопротивления Zн.

Будем считать, что размеры участка Dх, расположенного на расстоянии х от нагрузки линии, таковы, что полные изменения напряжения и тока на этом участке обусловлены исключительно его распределёнными параметрами DL, DR, DC и DG (рис. 6).

Пусть напряжение и ток в линии являются некоторыми функциями координаты х и времени t.

Тогда для любого произвольного момента времени t изменения напряжения, и тока на участке Dx могут быть выражены, с одной стороны, как

а с другой (см. рис. 6) –

Разложим 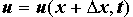и 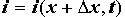в ряд Тейлора, ограничившись при этом двумя первыми членами разложения

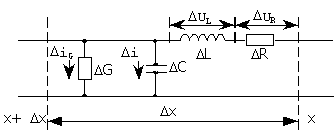
Рис. 5. Эквивалентная схема замещения линии передачи.

Подставляя (8) в (7) и (6) и учитывая (2), будем иметь

Приравнивая теперь правые части выражений (9) и (10) и пренебрегая членами, содержащими (Dx)², получим

Уравнения (11) впервые были получены В.Томсоном в связи с прокладкой и началом эксплуатации первого трансатлантического телеграфного кабеля и носит название “телеграфных уравнений”.

В случае рассогласования линии передачи, на конце длинной линии возникает отраженная волна. При разомкнутом конце линии отраженная волна имеет ту же фазу, что и падающая и в точке рассогласования возникает пучность напряжения. В случае короткого замыкания, в данной точке появляется пучность тока, а отраженная волна имеет противоположную фазу. В зависимости от длины линии (времени задержки) и длительности импульса возбуждения, волна отражения, суммируясь с прямой волной, изменяет форму фронта, спада и вершины импульсного сигнала при Т < Т, либо приводит к появлению дополнительных паразитных импульсов меньшей амплитуды.

Методика выполнения лабораторной работы:

1. Согласование линии и оценка ее длины.

а) Собрать схему передачи импульсного сигнала двухпроводной линией.

б) Установить параметры импульсного генератора: Т = 500 мкс (2кГц), А = 7 В, скважность 1:2 - 1:3.

Синхронизировать осциллограф для получения на экране 1 периода импульсного сигнала.

в) По времени прихода 1-го переотраженного импульса оценить время задержки распространения сигнала в линии при максимальном и минимальном R объяснить полученные эпюры напряжения и зарисовать их.

г) Подобрать R по минимуму искажений прямоугольного импульса и измерять R.

д) Объяснить схему подключения приборов.

2. Измерение затухания сигналов в линии на разных частотах.

а) Подключить вместо генератора импульсов в схеме п.1 ГСС. Установить уровень сигнала 0.3 В и измерять осциллографом уровень сигнала Uвх в согласованной линии на частоте 2 кГц.

б) Переключить осциллограф в конец линии параллельно R и измерять Uвых.

Затухание линии определяется соотношением:

в) Установить частоту генератора 20 кГц и повторить измерения.

3. Измерение полосы пропускания двухпроводной линии.

Измеряя амплитуду гармонического сигнала на выходелинии при изменении частоты от 2 кГц, определить полосу пропускания линии по уровню -6 дБ.

4. Исследование спектральных характеристик сигналов.

Спектры сигналов получают с помощью использования цифрового преобразования Фурье над оцифрованными выборками.

а) Параллельно осциллографу подключить вход звуковой карты, установленной в ПЭВМ, контролируя уровень сигнала (не более 0.5 В).

б) С помощью процедуры sb.exe записать гармонический сигнал с частотой 400 Гц. Частота дискретизации 20кГц.

в) Отключить вход звуковой карты от линии.

г) Вместо ГСС подключить генератор импульсов и проверить уровень сигнала. После чего, подключить вход звуковой карты. Установить частоту повторения 400Гц и скважность 1:2.

д) Записать выборку (б)). Повторить запись для скважности 1:10.

е) С помощью процедур MatLab рассчитать и построить спектры 3 сигналов.

Контрольные вопросы

1. При каком условии линия передачи считается длинной линией?

2. Какие элементы включает в себя эквивалентная схема бесконечно малого участка длинной линии?

3. Вывести дифференциальное уравнение длинных линий (“телеграфные уравнения”).

4. Что такое волновое сопротивление длинной линии? Коэффициент затухания? Фазовая постоянная?

5. Дать определение коэффициента отражения. Каким выражением связаны между собой коэффициент отражения и нагрузочное сопротивление линии?

Литература

1. Р. Тейлор. Шум. Москва. "Мир". 1998.

2. С.И. Баскаков. Радио/технические цепи и сигналы. Москва. "Высшая школа".2000.

3. С.И. Баскаков. Радиотехнические цепи с распределенными параметрами. Москва. "Высшая школа".2000.

4. Л. Френкс. Теория сигналов. Москва. "Советское радио". 1974.

5. М. Букенгем. Шумы в электронных приборах и системах. / Пер. с англ./- М.: Мир, 1986.